《数学物理方法》：连接数学与物理的桥梁

《数学物理方法》是理工科高年级本科生和研究生阶段的核心基础课程，也是理论物理、应用数学、工程科学等多个学科不可或缺的工具箱。该课程系统地讲授如何运用高等数学工具（如复变函数、积分变换、偏微分方程、特殊函数、变分法等）来建模、分析和求解物理问题，是连接抽象数学理论与具体物理现象的关键纽带。

为什么这门课如此重要？

在现代科学研究中，无论是量子力学中的薛定谔方程、电磁学中的麦克斯韦方程组，还是流体力学中的纳维-斯托克斯方程，其解析或数值求解都高度依赖《数学物理方法》中所涵盖的技巧。例如：

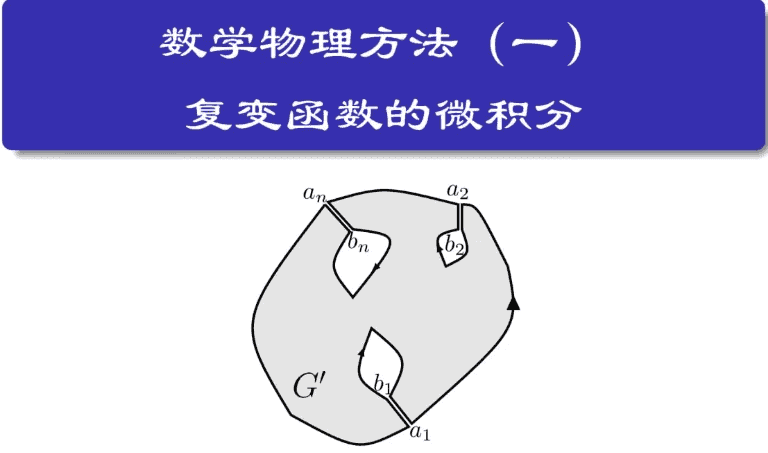
• 复变函数理论广泛应用于二维静电场、流体绕流问题以及量子散射理论；
• 傅里叶变换与拉普拉斯变换是信号处理、控制系统和热传导问题的核心工具；
• 分离变量法与格林函数法为求解各类偏微分方程提供了系统路径；
• 勒让德多项式、贝塞尔函数等特殊函数则是球坐标系或柱坐标系下物理问题的标准解。

学习难点与应对策略

许多学生反映该课程“抽象难懂”“公式繁多”“物理图像不清晰”。实际上，掌握《数学物理方法》的关键在于理解数学工具背后的物理动机。建议学习者：

• 结合具体物理问题（如振动弦、热传导、氢原子波函数）来理解数学方法的应用场景；
• 通过数值模拟（如使用Python或MATLAB）可视化解的结构，增强直观感受；
• 参考经典教材，如梁昆淼《数学物理方法》、Arfken & Weber《Mathematical Methods for Physicists》等，多角度理解概念。

前沿应用与跨学科价值

随着计算物理、人工智能与复杂系统研究的兴起，《数学物理方法》的知识体系正不断拓展其边界。例如，在机器学习中，格林函数思想被用于构建核方法；在量子计算中，特殊函数和群论方法用于设计量子算法；在地球物理与医学成像中，积分变换技术用于反演问题求解。掌握这些数学工具，不仅有助于夯实科研基础，也为跨学科创新提供强大支撑。

无论你是立志从事理论物理研究，还是希望在工程、数据科学或金融建模领域深耕，《数学物理方法》都将成为你学术与职业道路上的重要基石。